Batch Normalization

Batch normalization is a technique used to normalize the inputs of each layer in such a way that they have a mean of zero and a standard deviation of one.

The algorithm is relatively simple to implement:

• Values of $x$ over a mini-batch $B=\{x_1,x_2,\dots ,x_m\}$
• Outputs: $\{y_i=B{N}_{\gamma ,\beta }(x_i)\}$

We get the following equations:

$${\mu }_B=\frac{1}{m}\sum _{i=1}^m{x}_i$$

$${\sigma }_B^2=\frac{1}{m}\sum _{i=1}^m(x_i-{\mu }_B{)}^2$$

$${\hat{x}}_i=\frac{x_i-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}$$

$$y_i=\gamma {\hat{x}}_i+\beta$$

Where $\gamma$ and $\beta$ are learnable parameters that scale and shift the normalized value, respectively. $ϵ$ is a small constant to avoid division by zero.

The reason $\gamma$ and $\beta$ are learnable is that the network can learn to undo the normalization if it is not beneficial for the task at hand. Usually we set $\gamma =\sqrt{{\sigma }_B^2+ϵ}$ and $\beta ={\mu }_B$. This helps in the backward pass.

Inner workings §

Smoothness and Initialization

In the beginning, BatchNorm was introduced to solve the problem of internal covariate shift. This is the change in the distribution of network activations due to the change in the parameters of the previous layer. This makes training difficult as the network has to adapt to the new distribution of activations. This has been debunked by Santurkar et al. in their paper.

The real reason BatchNorm works is that it re-parameterizes the training process. It makes the significantly more smooth, thus ensuring the gradients are more stable and we can use a larger variety of learning rates. The main impact is the improvement in the Lipschitzness of a loss and gradients. The loss changes at a smaller rate and the magnitudes of the gradients are smaller too.

Smoothening effects impact the performance of the training algorithm in a major way. In deep neural networks, the loss function is not only non-convex but also tends to have a large number of “kinks”, flat regions, and sharp minimas. This makes gradient descent–based training algorithms unstable, e.g., due to exploding or vanishing gradients, and thus highly sensitive to the choice of the learning rate and initializations. BatchNorm reparametrization helps in making sure the direction of a computed gradient is a fair estimate of the true gradient direction. This stops the optimizer to take larger steps without the danger of sudden change in loss landscape. With this property, we can safely assume this makes the training significantly faster and less sensitive to hyperparameter choices.

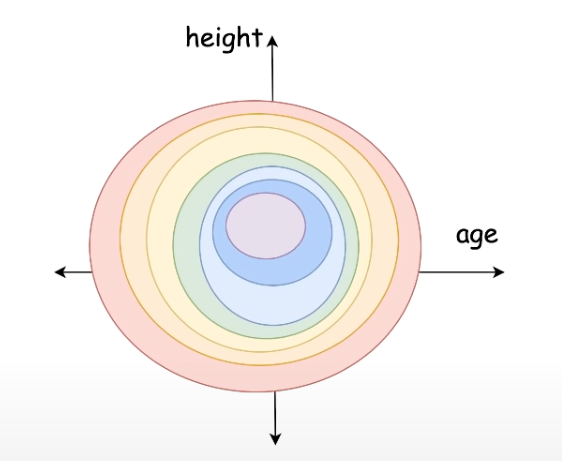
Let us assume you were training a model to predict if a mouse has cancer. We use the height and age as a predictor variables. We know the height of a mouse has lower variance than the age. If we don’t normalize the input, the model will learn to give more importance to the age than the height.

On the left, we can see the landscape before batchnorm. On the right side, we can see the landscape after batchnorm. The landscape is much smoother and the gradients are more stable.

Is this smoothening effect a unique feature of BatchNorm? §

The authors of the paper Santurkar et al. have shown that the smoothening effect is not unique to BatchNorm. The authors observe that $l_p$ regularization performs better than batchnorm. The reason is $l_p$ regularization lead to larger distributional shifs and yield improved performance.

References §

• Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
• How Does Batch Normalization Help Optimization?