Neural networks

Deep Neural Networks (DNNs) form the backbone of modern machine learning. One of the strength of DNNs is its high expressivity power. This capability to capture any flexible data representation allows deep neural networks to have widespread use from biology or weather prediction.

Universal Approximation Theorem §

Universal Approximation Theorem(UMT) states that any feedforward networks with a linear output layer, one hidden layer, activation function t can appoximate any continuous functions on a subset of $R^n$

Although a Feedforward Neural Network with a single layer can represent any function, the width has to be infinite. The UMT doesn’t guarantee whether the model can be learned or generalized properly.

Proof §

A neural network $C$ can model any function given a sample size $n$ and $d$ dimensions if: For every sample set $S\in R^d$ and $|S|=n$ and every function defined on this sample set $f:S->R$, we can find a set of weights such that $C(x)=f(x)$

Let us prove the simple case:

There exists a two-layer neural network with ReLU activations and $2n+d$ weights that can represent any function on a sample of size $n$ in $d$ dimensions.

First we would like to construct a two-layer neural network $C:{\mathbb{R}}^d\to \mathbb{R}$. The input is a $d$-dimensional vector, $x\in {\mathbb{R}}^d$. The hidden layer has $h$ hidden units, associated with a weight matrix $W\in {\mathbb{R}}^{d\times h}$, a bias vector $-b\in {\mathbb{R}}^h$ and ReLU activation function. The second layer outputs a scalar value with weight vector $v\in {\mathbb{R}}^h$ and zero biases.

The output of network $C$ for an input vector $x$ can be represented as follows:

$C(x)=v^{\top }\max \{Wx-b,0{\}}^T={\sum }_{i=1}^h{v}_i\max \{W_{(:,i)}x-b_i,0\}$

where $W_{(:,i)}$ is the $i$-th column in the $d\times h$ matrix.

Given a sample set $S=\{x_1,...,x_n{\}}^T$ and target values $y=\{y_1,...,y_n\}$, we would like to find proper weights $W\in {\mathbb{R}}^{d\times h}$, $b,v\in {\mathbb{R}}^h$ so that $C(x_i)=y_i$, ∀$i=1,...,n$.

Let’s combine all sample points into one batch as one input matrix $X\in {\mathbb{R}}^{n\times d}$. If set $h=n$, $XW-b$ would be a square matrix of size $n\times n$.

$M_{ReLU}=\max \{XW-b,0\}=\left[\begin{array}{c}\max \{x_{1}W-b\}\\ ...\\ \max \{x_{n}W-b\}\end{array}\right]=\left[\begin{array}{c}{x}_i{W}_{(:,j)}-b_j|x_i,j\end{array}\right]$

We can simplify $W$ to have the same column vectors across all the columns:

$W_{(:,j)}=w\in {\mathbb{R}}^d,\forall j=1,...,n$

Let $a_i=x_{i}w$, we would like to find a suitable $w$ and $b$ such that $b_1<a_1<b_2<a_2<\cdot \cdot \cdot <b_n<a_n.$ This is always achievable because we try to solve $n+d$ unknown variables with $n$ constraints and $x_i$ are independent. Set random $x_i$, sort the $a_k$ values. In between each $a_k$ set a $b_k$ value. Then $M_{ReLU}$ becomes a lower triangular matrix, due to the above condition.

$$M_{ReLU}=[a_i-b_j{]}_{i\times j}=\left[\begin{array}{ccccc}{a}_1-b_1& 0& 0& \dots & 0\\ ⋮& \ddots & & & ⋮\\ a_i-b_1& \dots & a_i-b_i& \dots & 0\\ ⋮& & & \ddots & ⋮\\ a_n-b_1& a_n-b_2& \dots & \dots & a_n-b_n\end{array}\right]$$

It is a nonsingular square matrix as $\det (M_{ReLU})\ne 0$, so we can always find suitable $v$ to solve $v{M}_{ReLU}=y$ (In other words, the column space of $M_{ReLU}$ is all of ${\mathbb{R}}^n$ and we can find a linear combination of column vectors to obtain any $y$).

You can also see the experimental results at UMT Proof

Why NN can even model noise? §

Since, we now know any NN are universal approximaters. We can safely assume that they are also able to learn unstructed noice perfectly.

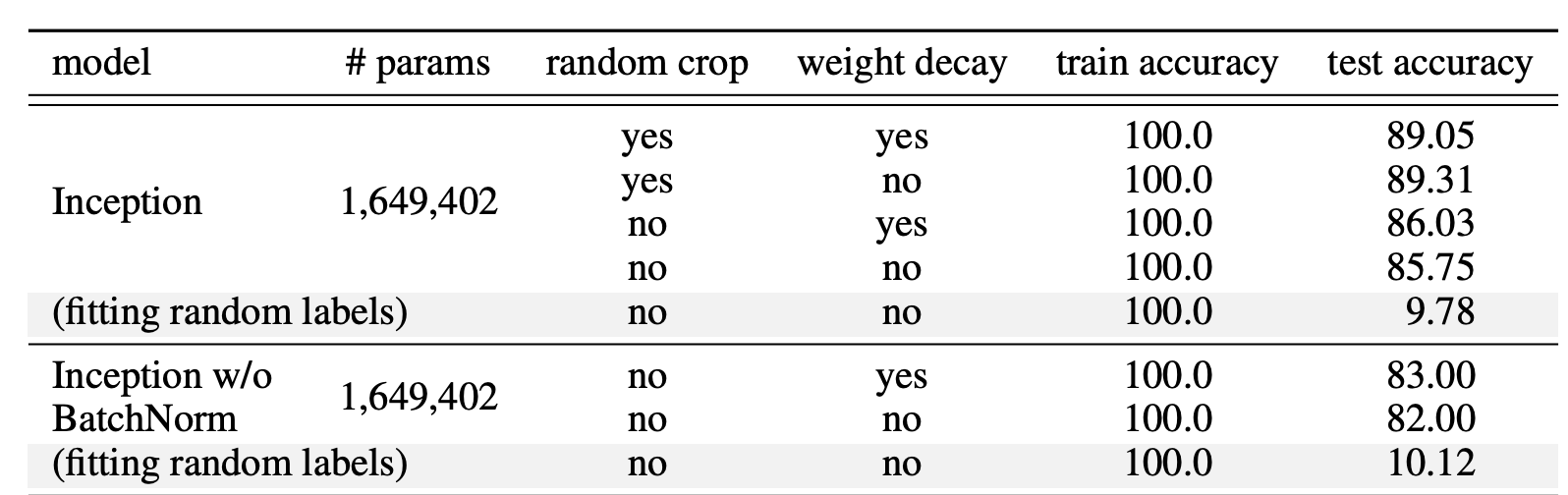
If labels of image classification dataset are randomly shuffled, the university principle of NN can still acheive net zero training loss. This doesn’t change with any degree of regularization.

Regularization is a not always the right answer §

Regularization is a common technique to prevent overfitting. However, it is works very differently in the context of neural networks. In contrast to traditional methods, regularization in neural networks acts as a tuning paramter that helps improve the test error. No single regularization seems to be critical independent of other terms. Thus, it is unlikely that regularizers are the fundamental reason for generalization.

Just move bro §

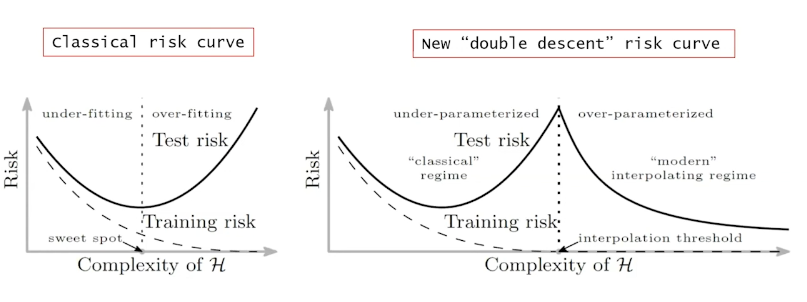
Considering a neural network with a great number of parameters, forming a high-dimensional parameter space, when learning happens on this high-dimensional objective landscape. The shape of the parameter space manifold is critical. For example, from the Batch Normalizations page, we can clearly see that a smoother manifold is benficial for optimization. It allows us to have more predictive gradients and larger learning rates.

Even though the parameter space is huge, fortunately we don’t have to worry too much about the optimization process getting stuck in local optima, as it has been shown that local optimal points in the objective landscape almost always lay in saddle-points rather than valleys. In other words, there is always a some dimensions containing paths to leave local optima and keep on exploring. As they say Just move bro.

There is some mindblowing math here specifically related to saddle points. Just to summarize:

• Critical points concentrate along a monotonically increasing curve in the $ϵ-\alpha$ plane.
• Eigenvalues do not seem to be exactly distributed according to the semicircular law, their distribution does shift to the left as the error increases
• A plateau around any critical point of the error function of a neural network.
• A trust region approach is a practical way to escape saddle points. This is done by making all the eigenvalues of the Hessian positive by adding a term $\alpha$ to the diagonal of the Hessian matrix. Rescale the gradient by the inverse of the modified eigenvalyes ( decrease the step size in general). To ensure descent along every eigen-directions, one must increase $\alpha$ until all the eigenvalues are positive.

Deep networks perform

Classic difference between NN and traditional ML §

Heterogeneous Layer Robustness §

Lottery ticket §

Neural tangent kernel §

Infinite width networks §

Deterministic NTK §

Linearized NTK §

Lazy training §

References: §

Source: 1 1/2 lessons of deep learning